はじめに
相関していることと、回帰分析の回帰係数が0でないことは概ね同じような感覚を持っていたけれど、もうちょっと違う理解の方がいいかもって感じた話。
- 相関係数: 2変数のばらつき方を表す指標
- 回帰係数: xからyを予測する回帰直線の係数で、あくまでx→yという話
NOTE: この記事では、相関係数はピアソンの相関係数、回帰係数はOrdinal Least Squares regression (OLS) で求める線形回帰の回帰係数について話します。
例
ちょっと極端な例かもしれないが、2つのデータセットを用意して、「回帰係数は変わらないけど相関係数は変わる」を具体的にします。
データA
y=xの関係でデータを作ります。
この場合、明らかに相関係数は1だし、回帰式も (当然だけど) y=xで回帰係数は1。
pacman::p_load(tidyverse, patchwork)
d1 <- data.frame(x = c(1:10), y = c(1:10))
plot1 <- ggplot(data = d1, aes(x = x, y = y)) +
geom_point() +
ggtitle("Data A") +
theme_bw()
plot1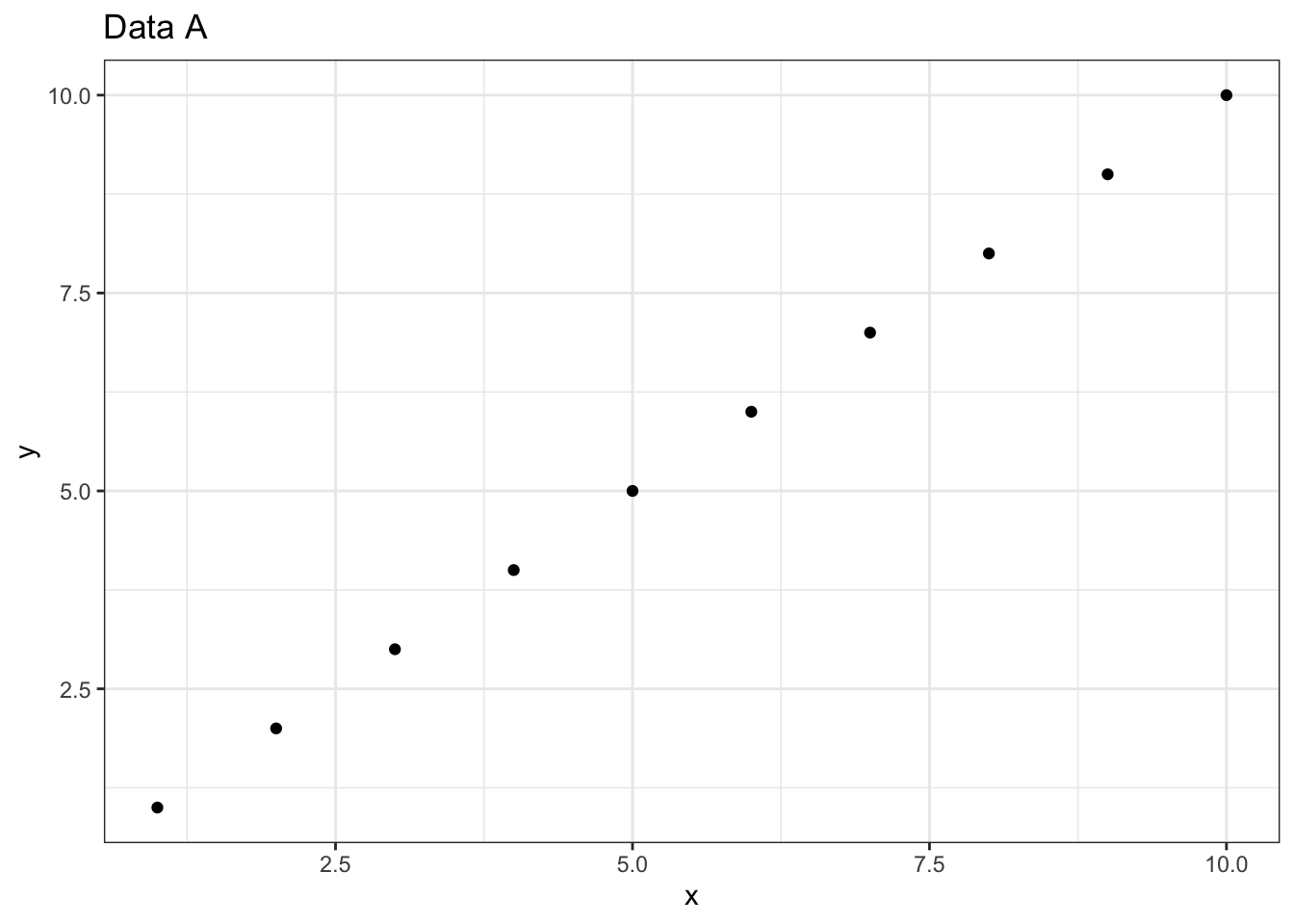
cor.test(d1$x, d1$y)##
## Pearson's product-moment correlation
##
## data: d1$x and d1$y
## t = 134217728, df = 8, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 1 1
## sample estimates:
## cor
## 1fit1 <- lm(y ~ x, data = d1)
summary(fit1)##
## Call:
## lm(formula = y ~ x, data = d1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.661e-16 -1.157e-16 4.273e-17 2.153e-16 4.167e-16
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.123e-15 2.458e-16 4.571e+00 0.00182 **
## x 1.000e+00 3.961e-17 2.525e+16 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.598e-16 on 8 degrees of freedom
## Multiple R-squared: 1, Adjusted R-squared: 1
## F-statistic: 6.374e+32 on 1 and 8 DF, p-value: < 2.2e-16データB
xが増えるとyも1増えるという関係はそのままに、y=x+interceptの切片の値をいくつか用意します。
xは1から10として、次のデータを用意
- y = x
- y = x + 10
- y = x + 20
- y = x + 30
d2 <- data.frame(x = rep(c(1:10), 4), y = c(1:10, 11:20, 21:30, 31:40))
plot2 <- ggplot(data = d2, aes(x = x, y = y)) +
geom_point() +
ggtitle("Data B") +
theme_bw()
plot2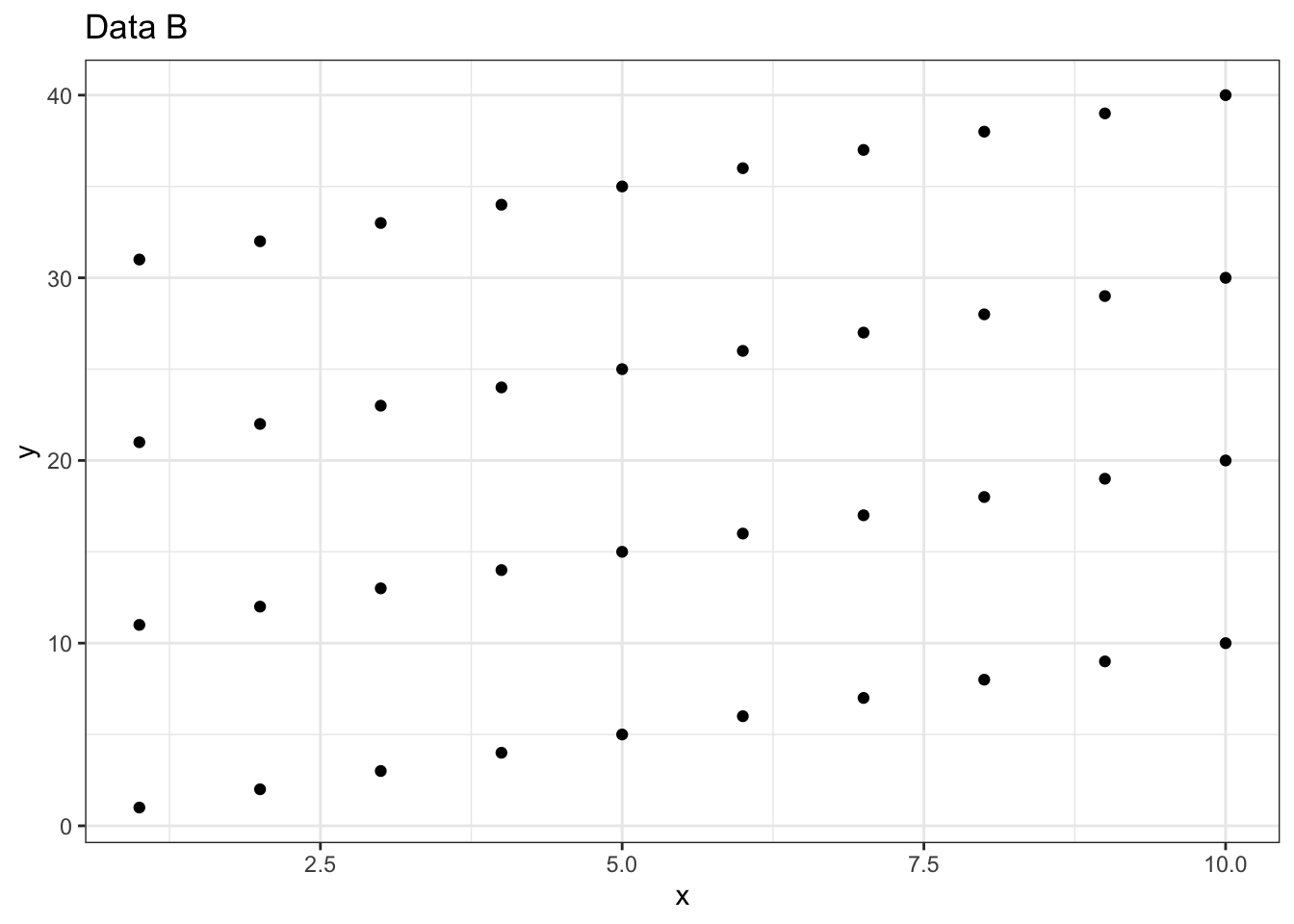
ここで相関係数の点推定値を確認すると、r=0.249 となり、先程のData Aとは大きく異なる数値となりました。
cor.test(d2$x, d2$y)##
## Pearson's product-moment correlation
##
## data: d2$x and d2$y
## t = 1.5837, df = 38, p-value = 0.1216
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.06795174 0.52002613
## sample estimates:
## cor
## 0.2488246一方、xの回帰係数の点推定値は1のままで、Data Aのときから変わりありません。
fit2 <- lm(y ~ x, data = d2)
summary(fit2)##
## Call:
## lm(formula = y ~ x, data = d2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.0 -7.5 0.0 7.5 15.0
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 15.0000 3.9180 3.828 0.000468 ***
## x 1.0000 0.6314 1.584 0.121558
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11.47 on 38 degrees of freedom
## Multiple R-squared: 0.06191, Adjusted R-squared: 0.03723
## F-statistic: 2.508 on 1 and 38 DF, p-value: 0.1216結果の整理
2つの分布を見るとこの通りです。
p1 <- plot1 +
ylim(c(0, 40))
plot1and2 <- p1 + plot2
plot1and2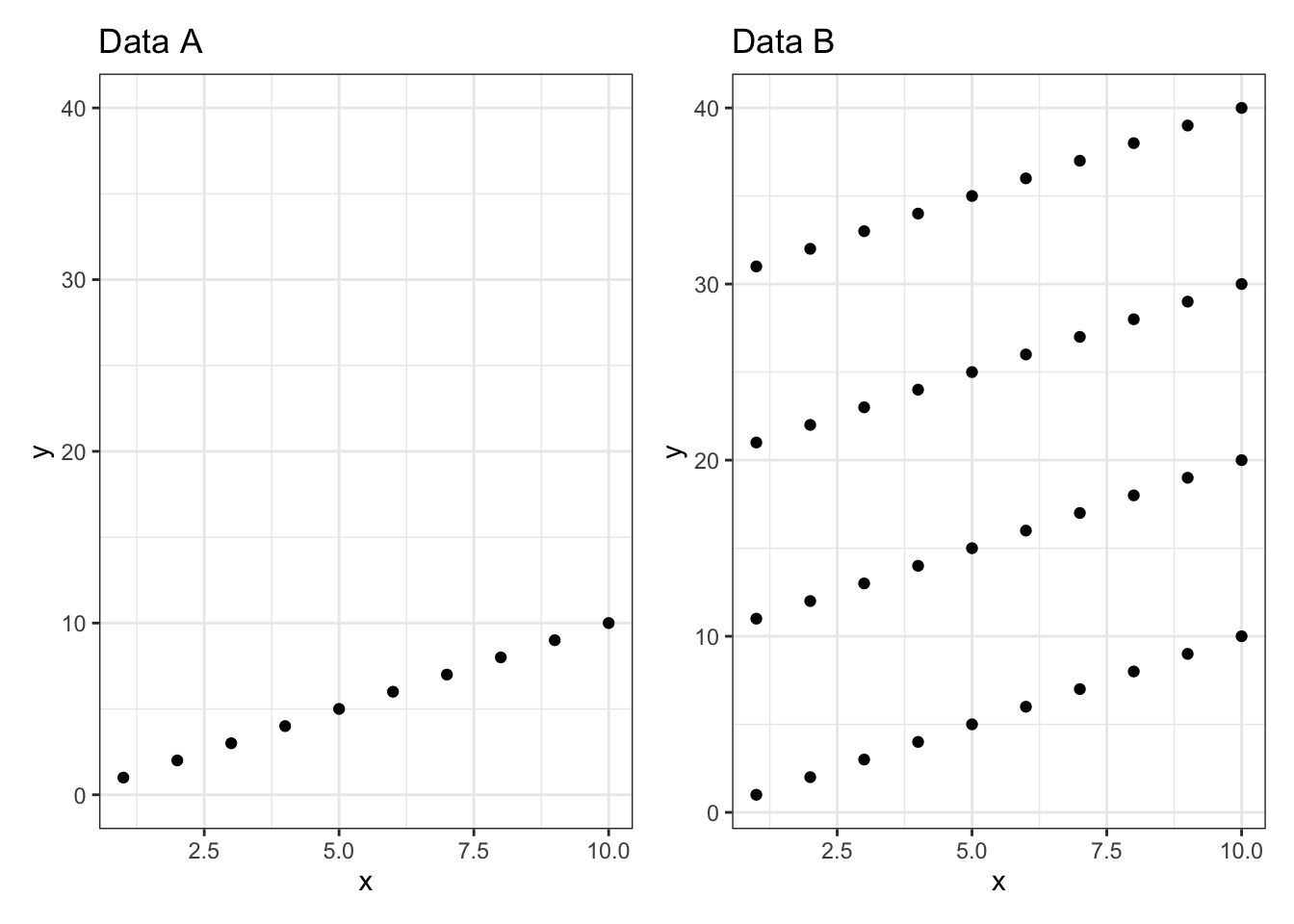
相関係数と回帰係数は以下。
| Data A | Data B | |
|---|---|---|
| 相関係数 | 1 | 0.2488246 |
| 回帰係数 | 1 | 1 |
回帰係数はデータAとBで同じなのに、相関係数は大きく違うことがわかります。
なんで相関係数は変わるの?
ピアソンの相関係数の計算式を再確認するとわかる話です。以下の式の通り、相関係数は共分散を各変数の標準偏差で割った値になります。
\[ r_{xy}=\frac{s_{xy}}{s_x ~ s_y} \] そこで、共分散・標準偏差を並べます。
| Data A | Data B | |
|---|---|---|
| 相関係数 | 1 | 0.2488246 |
| 共分散 | 9.1666667 | 8.4615385 |
| xの標準偏差 | 3.0276504 | 2.9088724 |
| yの標準偏差 | 3.0276504 | 11.6904519 |
yの分布がばらついたことで、相関係数の計算の分母が大きくなり、相関係数が0に近づいたと考えられます。
このように、相関係数はあくまで2変数のばらつき方の問題であって、x→yで考える回帰係数の考え方とは異なるものだと考えた方がいいのだろうと思います。
じゃ相関と回帰は完全に違うのか?
一方で、完全に異なる概念かというと、それは断じて違うと思います。
相関係数も回帰係数も、異なる計算を実行していますが、いずれも何らかの形で線形的な比例関係を捉えようとしているからです。 キーとなる要素は共分散です。
相関係数
共分散が軸となる概念です。共分散とは次の式で計算される値でした。
\[ s_{xy} = \frac{1}{n}\Sigma(x_i - \bar x)(y_i - \bar y) \]
ここで、総和する対象である各iの値がxとyの平均に対して、どの象限にあるかを考えましょう。
\[(x_i - \bar x)(y_i - \bar y)\]
共分散は、2つの変数 (x,y) が下図の+の象限に存在すれば正の方に傾き、逆もまた然り、という指標です。 そして、相関係数はxとyの標準偏差で割ることで取りうる値の範囲を-1から+1の間に規格化しているという指標になります。
plot1 +
geom_vline(xintercept = 5.5, linetype = 2, colour = "skyblue") +
geom_hline(yintercept = 5.5, linetype = 2, colour = "skyblue") +
annotate("text", x = 4, y = 2.5, label="+", size = 10, colour = "blue") +
annotate("text", x = 7, y = 2.5, label="-", size = 10, colour = "blue") +
annotate("text", x = 7, y = 7.5, label="+", size = 10, colour = "blue") +
annotate("text", x = 4, y = 7.5, label="-", size = 10, colour = "blue") +
ggtitle("concept of covariance")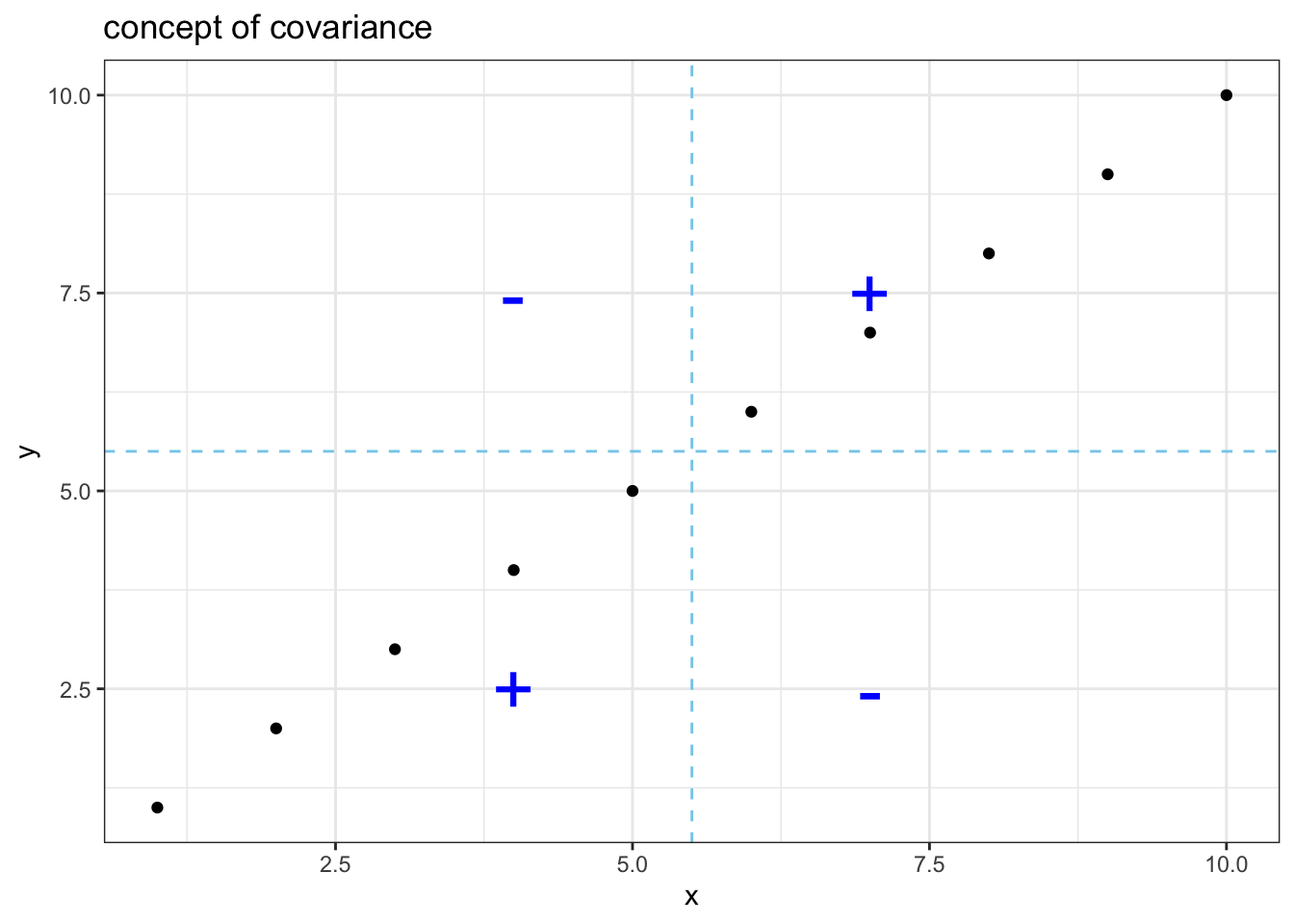
このことから、相関係数は共分散によって平均に対するデータの分布を評価し、xとyの標準偏差によってばらつき方を考慮するというプロセスで、変数間の関連を評価していると表現できます。
線形回帰の回帰係数
こちらはOLSなので、xからyを予測した際の残差eを最小にするというロジックで求められる値ですね。 大事なのは、「xからyを予測する」からスタートしていることであり、2変数のばらつきそのものに関心があるわけではないことです。
\[e_i = y_i - \hat {y_i}\]
回帰係数βの推定値は以下で表現できます。
\[ \hat \beta = \frac {\Sigma (x_i - \bar x)(y_i - \bar y)}{\Sigma (x_i - \bar x)^2}= \frac{s_{xy}}{\mathrm {Var}(x)} \]
ここでも共分散が登場するので、結局は同じような箇所に注目しているわけですね。
共分散と相関係数との関係を代入すると、次のような式変形も可能です。相関係数が登場しました。
\[ \hat \beta = \frac{s_{xy}}{\mathrm {Var}(x)}=r_{xy}\frac{s_y}{s_x} \]
統計的仮説検定の結果
p値は一致します。Data Bでのp値を確認します。
- 相関係数のp値: 0.1215579
- 回帰係数のp値: 0.1215579
したがって、点推定値の指す意味は違いますが、ざっくりと「比例関係あるんですか?」という結論ベース的には大まかに同じと言って問題ないんだろうと思います。
結局、相関と回帰は違うんですか???
非常に密接に関係しているし、統計的仮説検定の枠組みでいうと、単回帰とピアソンの相関係数の帰無仮説の棄却の結論は変わりません。
ただし、概念的には違うものと思った方がいいのだろうなあという、すっごいうるさい話でした。
- 相関係数: 2変数のばらつき方を表す指標
- 回帰係数: xからyを予測する回帰直線の係数で、あくまでx→yという話
そんじゃーね!