はじめに
最近共著の論文でpower関連の話題に出会ったので。 前回に引き続きpower関連の話です。
とりあえず、これ読みましょう→ Zhang, etal. 2019 めちゃくちゃおもしろいです。
Zhangらの主張は、こういう内容だと理解しました。
- 母集団の真値と、標本値は異なる→ そもそもpost-hoc power analysisが概念的に違う。
- 標本の値を使っているのに、あたかも真値かのようにpowerを計算するのは、精度よくない上に議論のミスリードをしてしまうこともあるのでは?
- post-hoc power analysisって何のためにやるのよ?なんか意味ある?
感想
- 言いたいこと、納得です。すごいなあ。
- けど、情報が乏しい中でbest availableなpowerの推論するなら、ある程度仕方ないのでは?
post hoc power analysisを自分でも回してみた
読んだら自作できそうだったので、自分でも試してみます。 設定はexposureもoutcomeも2値変数です (Zhangらはoutcomeが連続変数なので、少し違います。同じ議論ですが)
用語の設定を簡単にしておくと、
- 本来、prospective studyをする場合に事前にpower計算をして、リクルート数を決めます。ここで得られるpowerをprospective powerと呼びます。
- 対して、研究して効果の指標を得た後に、「このpowerってどの程度なの?」と事後にpowerを計算するシチュエーションがあります。ここで得たpowerをpost-hoc powerとします。
さて、今回実行した手順を簡単に言うとこんな形になります。
- イベント発生割合・リスク比を決める。これらの値は母集団の持つ真の値とする。
- 研究参加者数を決めて、1に従うデータを作成する。(神のみぞ知る値を知った状態で、サンプリングしてくるってイメージ)
- 2で得たデータでリスク比を計算して、powerを計算する
- 2-3を何度も繰り返してpost-hoc powerの分布を得る
研究参加者数や効果/関連が大きくなるほど、prospective powerとpost-hoc powerは等しくなるはずです。 では、研究参加者数が少なかったり、効果が小さい場合はどうなるのでしょう?実際に見ていきましょう。
ちょっとテクニカルな話
コードの中身について
- Monte-Carlo simulation, default number of iterations = 10,000
- 値を指定すると、ggplotで作った図を返します
- powerは{pwr.2p2n}で取得しました
pacman::p_load(pwr, tidyverse)
Visualize_PosthocPowerAnalysis <- function(n1, n2, prob1, prob2, itr=10000){
true_power_res <- pwr.2p2n.test(h = ES.h(p1 = prob1, p2 = prob2),
n1 = n1, n2 = n2,
sig.level = 0.05,
alternative = "two.sided")
true_power <- true_power_res[["power"]]
posthoc_power <- numeric(itr)
for (i in 1:itr) {
set.seed(i)
sample_prob1 <- rbinom(1, n1, prob1)/n1
sample_prob2 <- rbinom(1, n2, prob2)/n2
posthoc_power_res <- pwr.2p2n.test(h = ES.h(p1 = sample_prob1, p2 = sample_prob2),
n1 = n1, n2 = n2,
sig.level = 0.05,
alternative = "two.sided")
posthoc_power[i] <- posthoc_power_res[["power"]]
}
data <- data.frame(posthoc_power = posthoc_power)
# description for data viz
cha1 <- sprintf("true value of event probability: control group=%.2f", prob1)
cha2 <- sprintf(", exposed group=%.2f\n", prob2)
cha3 <- sprintf("number of participants: control group=%d", n1)
cha4 <- sprintf(", exposure group=%d\n", n2)
cha5 <- sprintf("%.3f", true_power)
subtitle <- paste0(cha1, cha2, cha3, cha4)
caption <- paste0("hashed line: true power (=", cha5, ")")
# visualize data using ggplot2
plot <- ggplot(data = data, aes(x = posthoc_power)) +
geom_histogram() +
geom_vline(xintercept = true_power, linetype = 2, size=1, colour = "red") +
labs(title = "Histogram of post-hoc power, along with true power, based on Monte Carlo method",
subtitle = subtitle,
caption = caption) +
theme_bw()
return(plot)
}関数の説明と実行
説明が重複しますが、一応。
コントロール群・曝露群の人数と、それぞれの真のイベント発生割合 (母集団でそのようなイベント発生割合が得られる、と仮定) を入力すると、true power (1つの値) & post-hoc powerの分布 (1万回の試行から取得) を返します。なお、post-hoc powerは、真の値に従ってサンプリングされたデータから計算されます。
引数の説明は以下の通りです。
- n1: コントロール群の人数
- n2: 曝露群の人数
- prob1: コントロール群のイベント発生割合
- prob2: 曝露群のイベント発生割合
じゃあ、実際に図を描きながら、以下の内容を確認します。
post-hoc powerは、a) 研究参加者数が少ない、または b) 効果が小さい場合、prospective powerに対してばらついた値を返す
今回は例を3つ作成し、効果の値は一定としつつ人数を変えていきます。なお、効果の大小を変更しても同じ結論になります。
例1: 各群200人
各群200人 (合計400人)、コントロール群でイベント発生割合が10%, 曝露群で15% (i.e., risk ratio = 1.5) とします。
下の図を見てください。例1の設定では、真のpower (= prospective power) は0.33です。 一方、この設定で得られたサンプリングされた集団で得たpost-hoc powerは0付近から1.0近くまで、非常に様々な値を取ります。 また、post-hoc powerの最頻値もprospective powerから乖離していますね。
実際にpost-hoc powerを計算する場合は、たった1つの値を得るだけです。今回のように分布を得るわけではありません。 そうなると、post-hoc powerの1つの値を見たところで、何も言えないなーって感じしちゃいますよね。 prospective powerの参考とするには、あまりに粗い指標と言えそうです。
Visualize_PosthocPowerAnalysis(n1 = 200, n2 = 200,
prob1 = 0.1, prob2 = 0.15)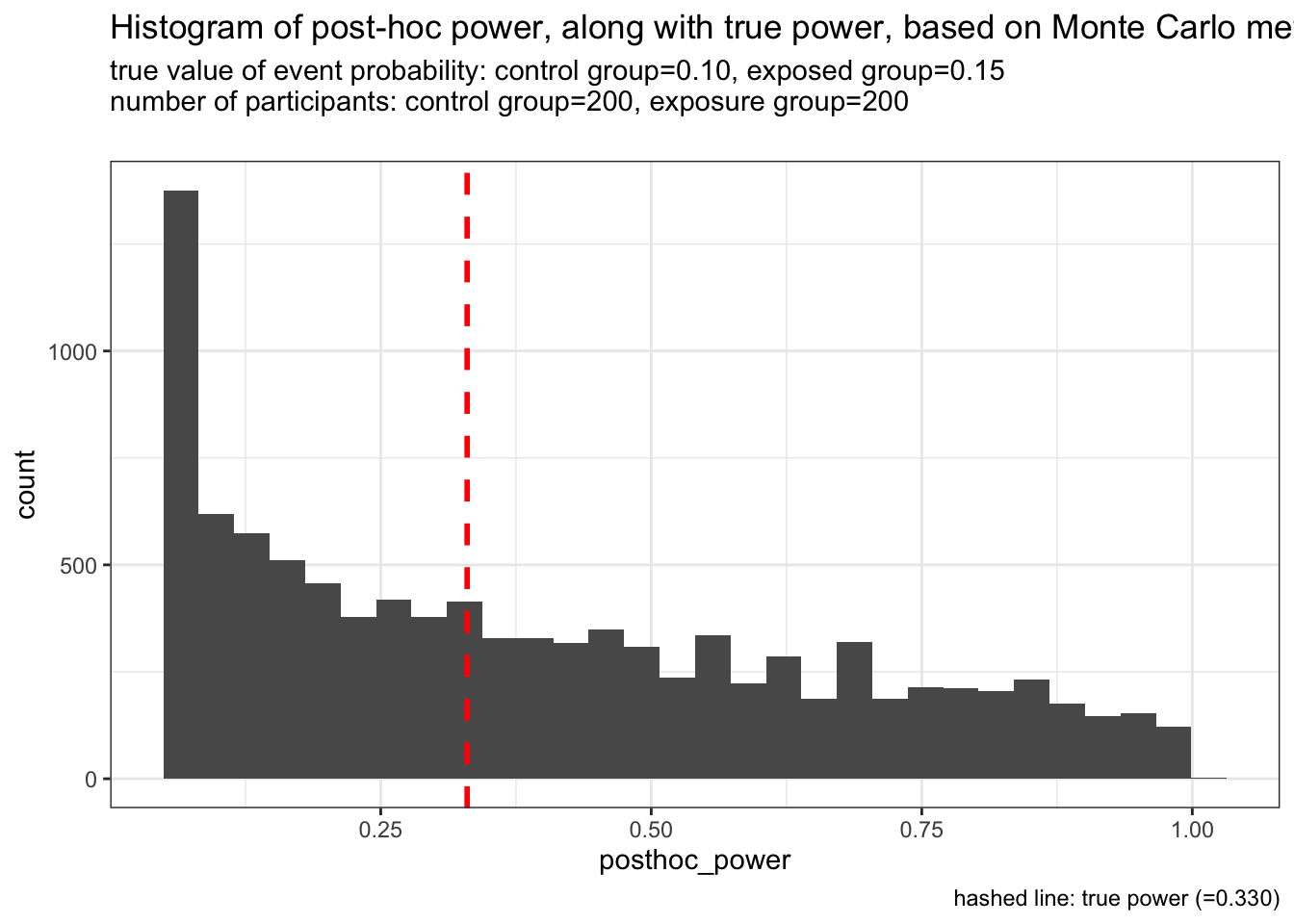
例2: 各群650人
もう少し人数を増やします。prospective powerが0.8近くになるよう、各群650人 (合計1300人) としました。この状況でも、post-hoc powerはかなりばらついた分布を取ります。
Visualize_PosthocPowerAnalysis(n1 = 650, n2 = 650,
prob1 = 0.1, prob2 = 0.15)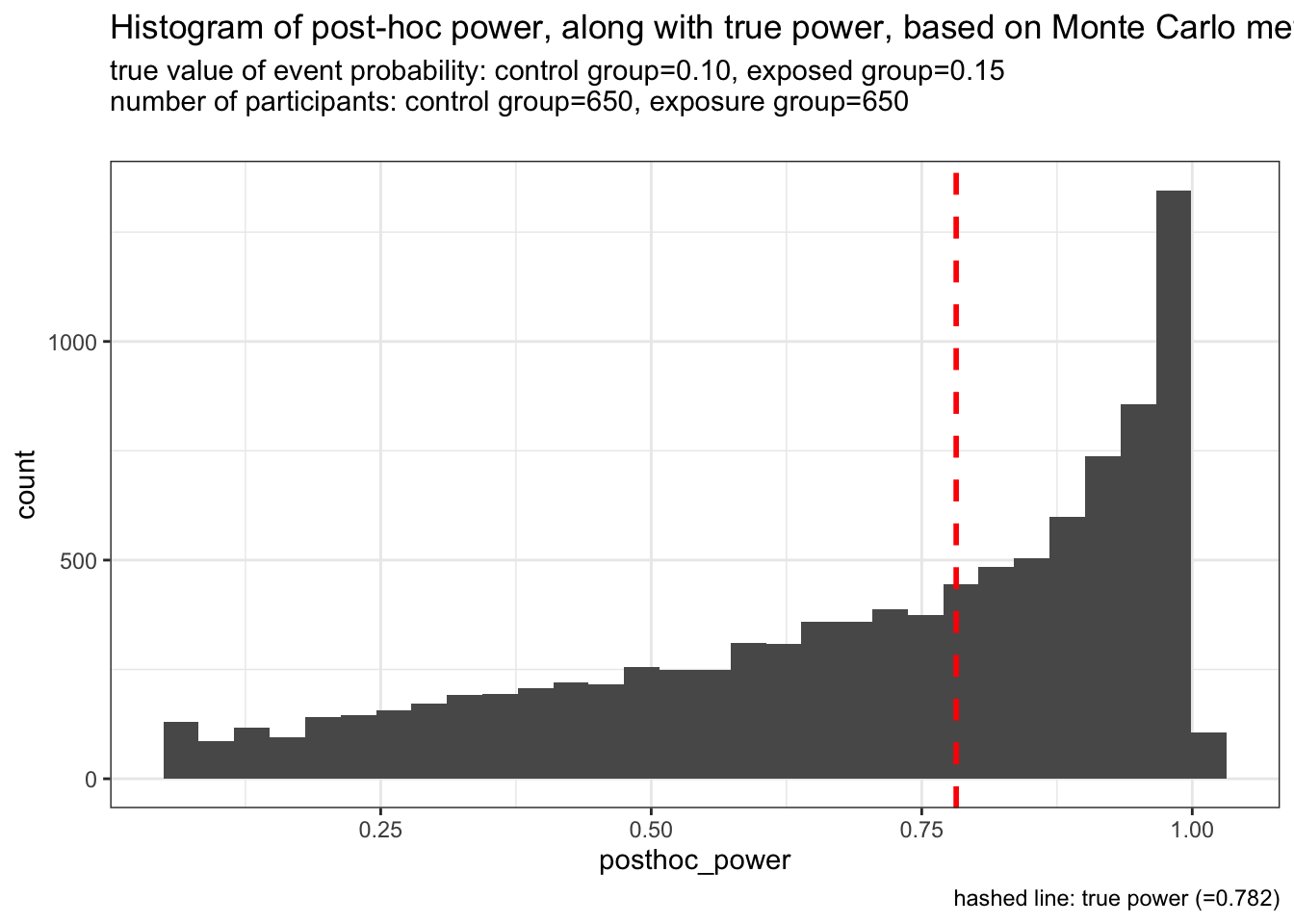
例3: 各群1000人
やけくそ気味に各群1000人 (合計2000人) としました。prospective power=0.925です。
こうなると、かなりprospective powerとpost-hoc powerが近くなることがわかります。 ただprospective powerが0.925と、ほぼほぼ有意と判断される状況ですから、post-hoc power analysisをしたい状況ではないような気がします。
Visualize_PosthocPowerAnalysis(n1 = 1000, n2 = 1000,
prob1 = 0.1, prob2 = 0.15)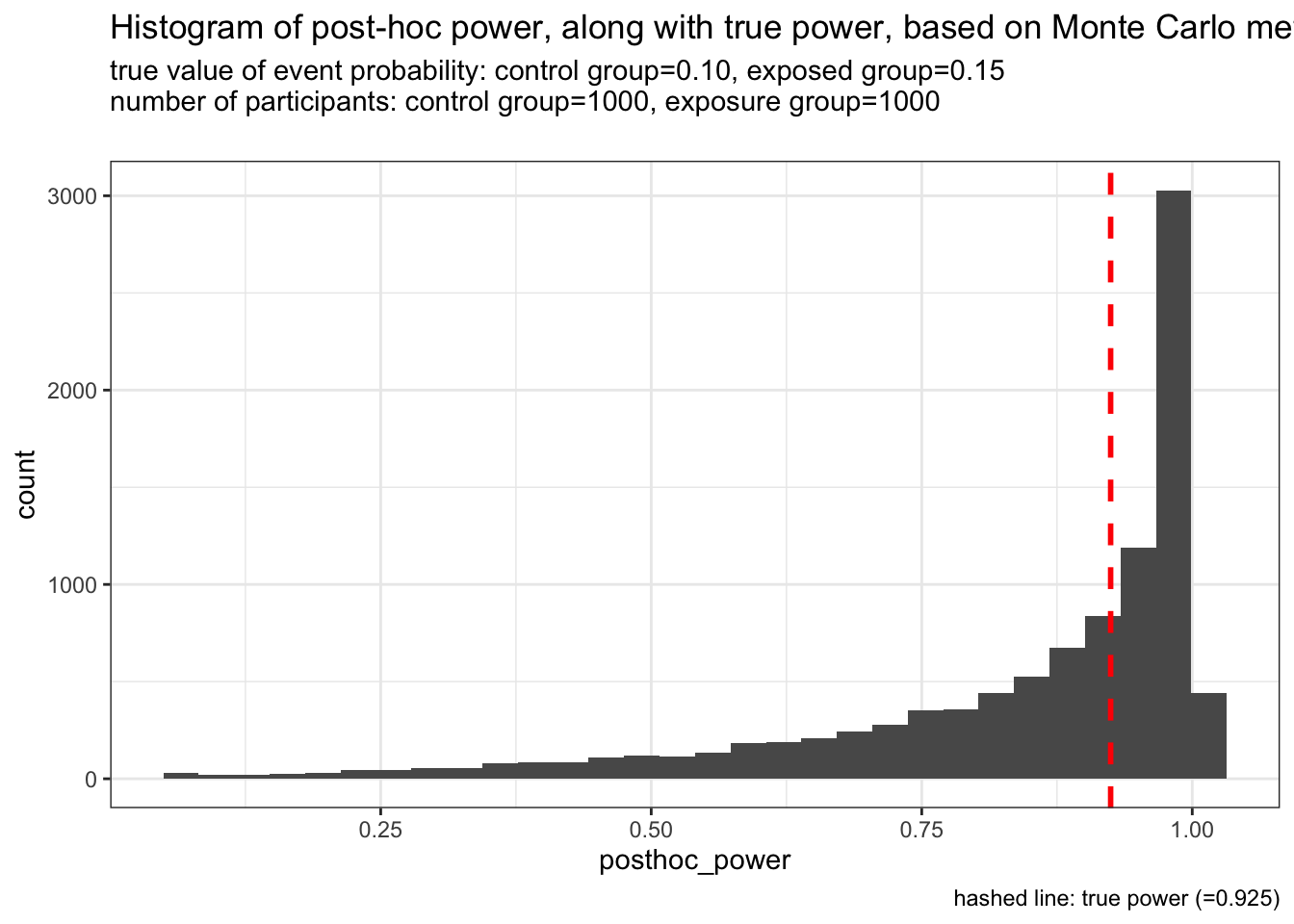
まとめと感想
まずは Zhang, etal. 2019 を読んだ & 自分でも図を作った感想。
- 「標本集団で得られた標本値を、あたかも母集団の真の値かのように使ってpowerを計算するのは、概念的に間違っている」という指摘はごもっとも。
- post-hoc powerは、a) 研究参加者数が少ない、または b) 効果が小さい場合、prospective powerに対してばらついた値を返す、ということを再現。納得。
したがって、査読コメントで「post-hoc power計算してください」は結構ミスリーディングな議論になりえるトピックなんだなあと思いました。
でも先行研究が非常に乏しい中prospective powerを得たい場合って、post-hoc powerの計算とやってる行為自体は一緒では…? とも感じました。 こういう場合、どうするのが正解なんでしょうか?
まず、先行研究が乏しい状況では、そもそも真の値を考えること自体が変な気がしますね。ベイズ的議論が必要そう。あるいはもっとシンプルに、いくつか試すとか。例えばこんな感じ。
- 真のリスク比はわからない→ いくつかのリスク比を試す
- power≥0.8を達成できる、許容されるサンプルサイズの幅を得る
→ 証拠がそれほどない場合、powerを1つのpoint estimateで考えるのがよくないのであって、「真の値を知らない→ いくつかのシナリオを置こう」と、ばらつきを伴って理解するべきでは?
以上、最近の勉強でした。