はじめに
「稀な疾病の場合、オッズ比はリスク比に近似できる」とは、疫学を勉強した人なら聞いたことがあるはずのフレーズです。
しかし、「稀な疾病」とはどの程度稀なのでしょうか?
今回は、リスク比とオッズ比を様々なイベント発生割合で比較します。
伝えたいこと
Risk Ratio (RR) とOdds Ratio (OR) の関係に関して
- RR>1 のとき、イベント発生割合が大きくなるほど(i.e. イベントがcommonになるほど)、ORはRRより大きくなる。
- リスク比・オッズ比が大きくなるほど、リスク比・オッズ比の乖離は大きくなる。
- イベント発生割合が10%が一般的なthreshold。10%を超える場合は、オッズ比ではなくリスク比を使うことを考える。
→ なんでもかんでも、「2値アウトカムにロジスティック回帰」はダメなんじゃない…?(次回以降)
基本の確認
リスク比・オッズ比
コホート研究を通して、次の2×2表が得られたとします (横断研究でオッズ比vs有病率比を考える際も同じ議論です)。
| イベントあり (人) | イベントなし (人) | 合計 (人) | |
|---|---|---|---|
| 曝露あり | a | b | N |
| 曝露なし | c | d | M |
リスク比とは、次の計算式で得られる値です。
イベントが発生した人の割合を、それぞれの群で計算し、比をとったものとなります。
\[\mathrm{RiskRatio}=\frac{p_1}{p_2}=\frac{\frac{a}{a+b}}{\frac{c}{c+d}}=\frac{a/N}{c/M}=\frac{aM}{cN}\] where
\[p_1 = \frac{a}{N},~p_2 = \frac{c}{M}\]
一方、オッズ比とは、次の計算式で得られる値です。 イベントのオッズの比ですね。
\[\mathrm{OddsRatio} = \frac{\frac{p_1}{1-p_1}}{\frac{p_2}{1-p_2}}=\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{ad}{bc}\]
「稀な疾病」の仮定と、オッズ比≒リスク比の導出
ここで、イベントが稀な場合、オッズ比がリスク比に近似できるという導出を行います。
稀な疾病の仮定は、英語では”rare disease assumption”と言います。(そのままですが、知らないと検索しにくい)
イベントが稀な場合、2×2表においてa,cがb,dに対して十分小さい、と考えることができます。
「a,cがb,dに対して十分小さい」という仮定から、a/Nやc/Mが1に対して十分小さいと考えると、以下のような計算ができます。
\[
\mathrm{OddsRatio} = \frac{ad}{bc} = \frac{a(M-c)}{c(N-a)}=\frac{aM(1-\frac{c}{M})}{cN(1-\frac{a}{N})}\simeq \frac{aM}{cN}=\frac{\frac{a}{N}}{\frac{c}{M}}=\mathrm{RiskRatio}
\]
「稀な」疾病とは、どの程度稀なのか?
集団でのイベント発生割合が稀であると仮定できるとき、オッズ比≒リスク比と考えることができます。
しかしながら、稀とはどの程度なのでしょう?
10%は稀?それとも30%くらいまで稀と言っていいのでしょうか?
今回はこの疑問に答えていきます。
リスク比とオッズ比との関係
まずはこの図を見てください (この図がとても重要です)。
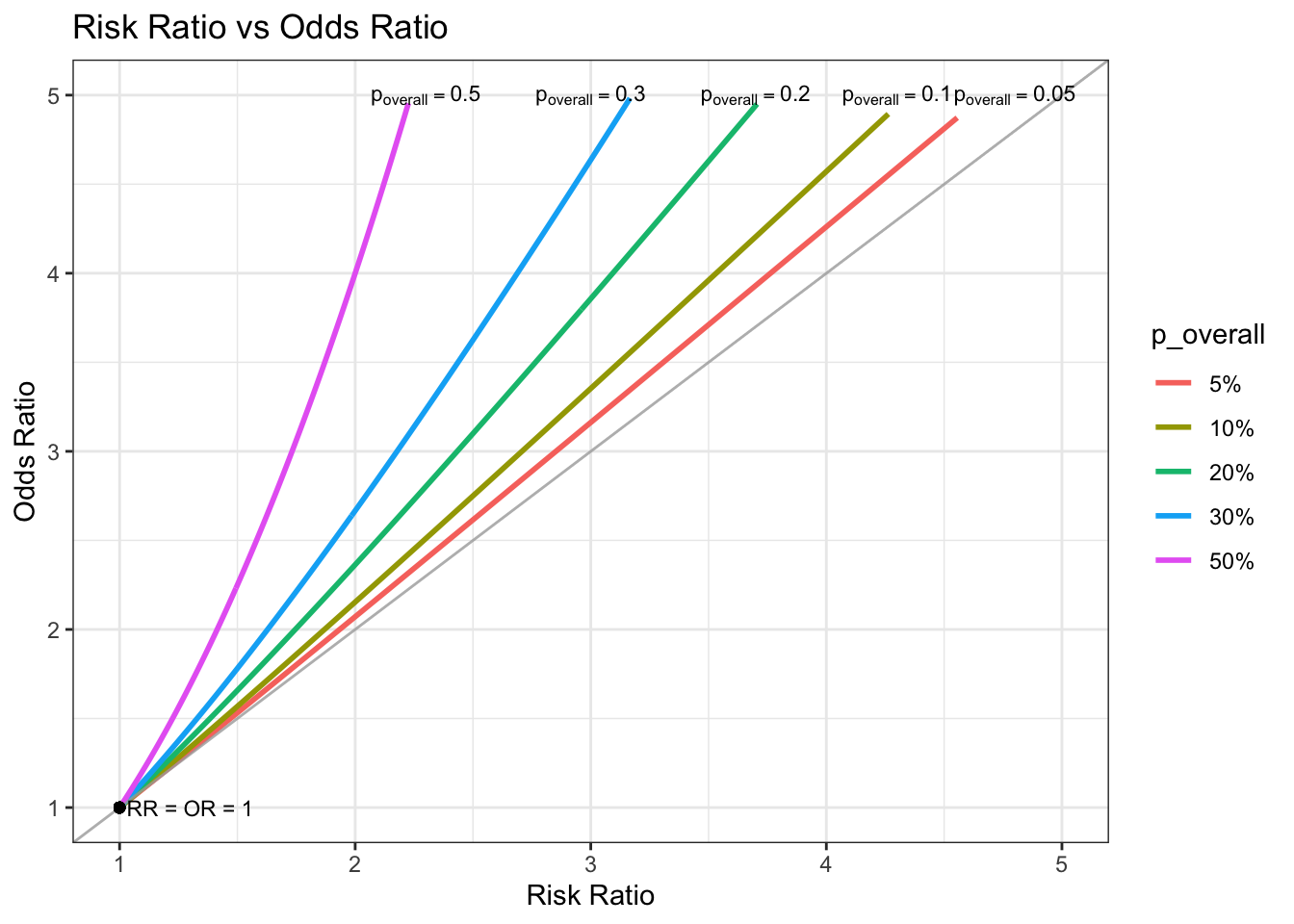
この図は横軸にリスク比、縦軸にオッズ比を取っており、p_overallは集団におけるイベント発生割合を示します。
見方としては、グラフ中のグレーの直線 (y=xの直線) に対して近いほど、リスク比とオッズ比との乖離が小さいことを表します。
例えば、p_overall=0.5 (1番左側の線) はy=xから大きく乖離している一方、
p_overall=0.05 は y=x とほぼ同じで、リスク比とオッズ比がほぼ同じ (近似できる) ことを意味しています。
こう見ると、イベント発生割合が20%くらいから、リスク比とオッズ比の乖離が目立つことがよくわかりますね!
具体的な値を確認してみましょう。リスク比が1.5の場合、オッズ比は次の値を取ります。
| 集団のイベント発生割合 | リスク比 | オッズ比 |
|---|---|---|
| 5% | 1.5 | 1.5 |
| 10% | 1.5 | 1.6 |
| 20% | 1.5 | 1.7 |
| 30% | 1.5 | 1.8 |
| 50% | 1.5 | 2.3 |
もう1つ例を確認します。リスク比が2.0の場合のオッズ比は次のとおりです。
| 集団のイベント発生割合 | リスク比 | オッズ比 |
|---|---|---|
| 5% | 2.0 | 2.1 |
| 10% | 2.0 | 2.1 |
| 20% | 2.0 | 2.4 |
| 30% | 2.0 | 2.7 |
| 50% | 2.0 | 4.0 |
2つの表を見ると、リスク比が大きいほどリスク比とオッズ比との乖離が大きくなることもわかりました。
以上から、イベント発生割合が10%程度なら、通常のリスク比の範囲であればOR≒RRといって問題ないだろう、というように思います。
イベント発生割合が10%を超え20%, 30%となっているならば、リスク比とオッズ比の乖離具合を考えた方がよいのかなと思います。
まとめ
Risk Ratio (RR) とOdds Ratio (OR) の関係に関して
- RR > 1 のとき、イベント発生割合が大きくなるほど(i.e. イベントがcommonになるほど)、ORはRRより大きくなる。
- リスク比・オッズ比が大きくなるほど、リスク比・オッズ比の乖離は大きくなる。
- 一般に、稀と判断されるのはイベント発生割合が10%以下の場合である。
今回の内容を踏まえると、イベント発生割合によってはロジスティック回帰の使用に慎重になるべきことがわかります。
2値アウトカムの研究に関しては、ロジスティック回帰が多用される傾向にあります。
しかしながら、イベント発生割合が高いとORがRRよりも大きくなってしまい、近似することが難しくなってしまいます。
このような場合、効果の指標としてのオッズ比の妥当性が乏しくなってしまい、オッズ比よりもリスク比の方が指標として望ましい、と考えられます。
(もちろんオッズ比としての議論は可能ですが、リスク比の方が科学的・社会的実用性が高い以上、やはりリスク比と近似できる状況でのオッズ比が望まれるわけです)
したがって、イベント発生割合が10%を超えるような状況では、修正ポアソン回帰やlog-binomial回帰などが分析手法の候補となります。これらについては別の回に紹介しますね。
今回の記事では、「稀なイベントとはイベント発生割合が10%以下である」を深堀りし、
リスク比とオッズ比との乖離を確認しました。
それでは、おつかれさまでした。
付録: グラフの作成方法
付録として、今回の議論の仮定および題材作りのコードをシェアします。
knowledge consumersとしてはややハイレベルな議論かもしれませんが、knowledge creatorsを目指す人はぜひご一読ください。
データづくり
観察集団が曝露群1000人・非曝露群1000人、合計2000人いたとします。
また、集団全体のイベント発生割合p_overall(観察集団全体のリスク)は次の5通りで進めていきます。
- 5%
- 10%
- 20%
- 30%
- 50%
2×2表は次のとおりです。
| イベントあり (人) | イベントなし (人) | 合計 (人) | |
|---|---|---|---|
| 曝露あり | a | 1000-a | 1000 |
| 曝露なし | c | 1000-c | 1000 |
ここで、集団全体のイベント発生割合は次の式を満たします。
\[p_{overall} = \frac{a+c}{2000}\]
よって、以下の通り変形することができます。
\[c = 2000\cdot p_{overall}-a\]
したがって今回の2×2表の研究結果は、p_overallが与えられれば、aの関数として表現することができますね。
リスク比とオッズ比は次の通りです。
(リスク比とオッズ比がそれぞれaとp_overallの2つの文字で表現できていることを確認してください。p_overallは定数とするので、aの関数となります)
\[ \mathrm{RR} = \frac{a/1000}{c/1000} =\frac{a}{c} = \frac{a}{2000p_{overall} - a} \]
\[ \mathrm{OR} = \frac{a\times (1000-c)}{c\times (1000-a)}=\frac{a(1000+a-2000p_{overall})}{(1000-a)(2000p_{overall}-a)} \]
ただし、次を満たします。
- aは、1≤a≤999を満たす自然数
- RRは1以上 (RR<1は逆数を取ればよいため)
- ORは1以上
これをコードとして実装していきましょう。
pacman::p_load(tidyverse)
a <- c(1:999)
d0 <- data.frame(a)
d0 <- d0 %>%
# set overall risk
mutate(p1 = 0.05) %>%
mutate(p2 = 0.1) %>%
mutate(p3 = 0.2) %>%
mutate(p4 = 0.3) %>%
mutate(p5 = 0.5)
df <- d0 %>%
pivot_longer(cols = p1:p5,
names_to = "p_overall",
values_to = "p") %>%
mutate(RR = a/(2000*p - a)) %>%
mutate(OR = a*(1000+a-2000*p)/((1000-a)*(2000*p-a)) ) %>%
mutate(p_overall = case_when(
p_overall == "p1" ~ "5%",
p_overall == "p2" ~ "10%",
p_overall == "p3" ~ "20%",
p_overall == "p4" ~ "30%",
p_overall == "p5" ~ "50%"
),
p_overall = factor(p_overall, levels = c("5%", "10%", "20%","30%", "50%")))現在の段階では、リスク比やオッズ比が負の値や無限大(0割りの結果)となる場合も含まれるので、除外して整理します。
また、RRやORの範囲が現状だと広すぎるので、上限を5とします。
- 1 ≤ RR ≤ 5
- 1 ≤ OR ≤ 5
df <- df %>%
filter(RR >= 1 & OR >= 1 & RR <= 5 & OR <= 5)リスク比 vs オッズ比のグラフ作り (ggplot2)
データづくりが完了したので、グラフ化しましょう。(大事なポイントです)
plot <- ggplot(data = df, aes(x = RR, y = OR, group = p_overall, colour = p_overall)) +
geom_line(size = 1) +
geom_abline(slope = 1, intercept = 0, alpha = 0.8, colour = "darkgray") +
geom_point(x = 1, y = 1, colour = "black") +
scale_x_continuous(limits = c(1, 5)) +
scale_y_continuous(limits = c(1, 5)) +
xlab("Risk Ratio") +
ylab("Odds Ratio") +
ggtitle("Risk Ratio vs Odds Ratio") +
annotate("text", x = 2.3, y = 5, label = "p[overall] == 0.5", size = 3, parse = TRUE) +
annotate("text", x = 3, y = 5, label = "p[overall] == 0.3", size = 3, parse = TRUE) +
annotate("text", x = 3.7, y = 5, label = "p[overall] == 0.2", size = 3, parse = TRUE) +
annotate("text", x = 4.3, y = 5, label = "p[overall] == 0.1", size = 3, parse = TRUE) +
annotate("text", x = 4.8, y = 5, label = "p[overall] == 0.05", size = 3, parse = TRUE) +
annotate("text", x = 1.3, y = 1, label = "RR = OR = 1", size = 3) +
theme_bw()
plot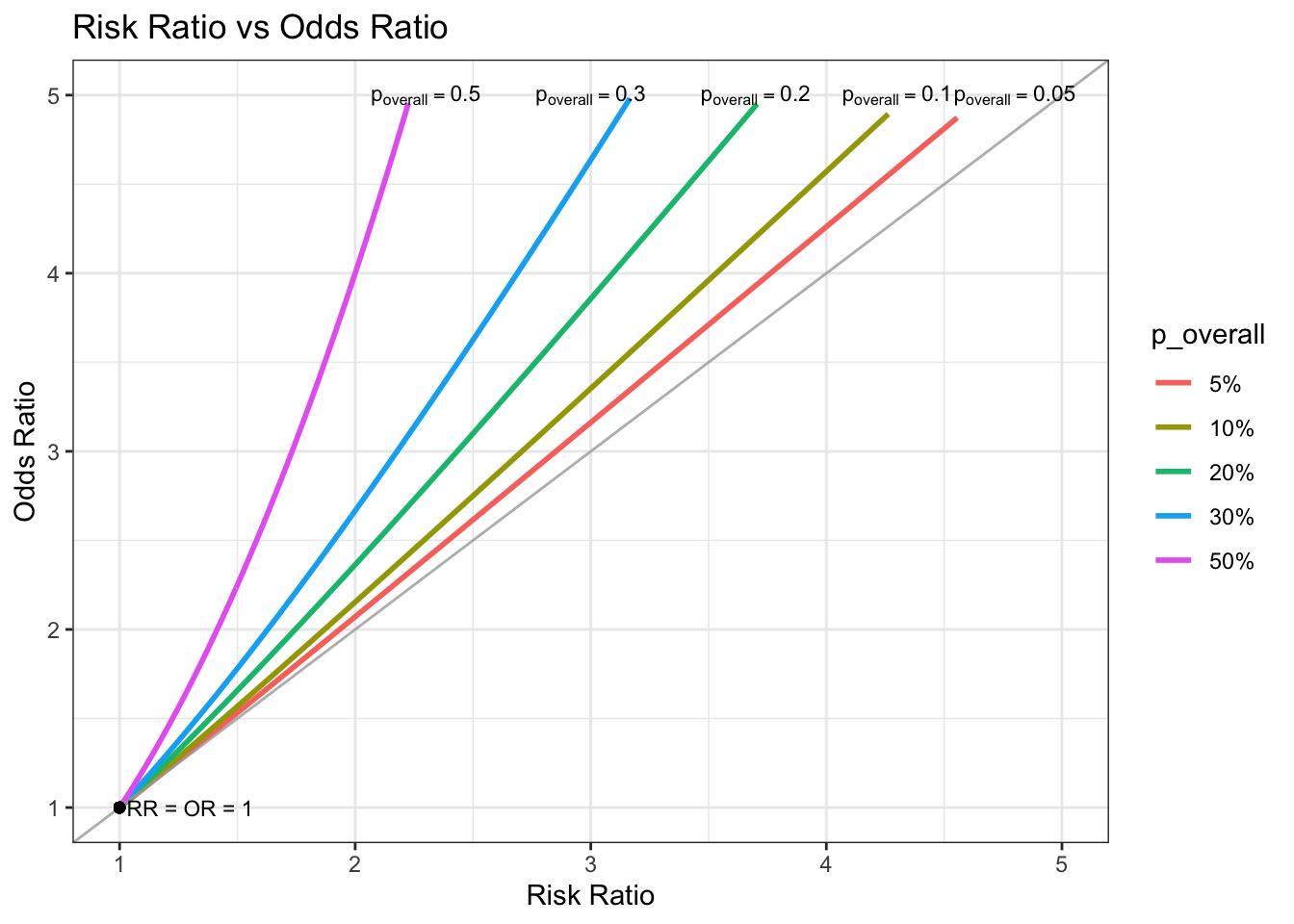
# ggsave(file = "output/RiskRatio_vs_OddsRatio.png", plot = plot, dpi = 300, width = 7.5, height = 5)具体的な値を確認するコードは次のとおりです。
FYI: 与えられた値に対して最も近い値を返す -> 差分の絶対値が最小のものをgroup_byして取ればよい
df %>%
filter(round(RR, digits = 2) == 1.5) %>%
group_by(p_overall) %>%
filter(abs(RR-2) == min(abs(RR-2)))## # A tibble: 5 × 5
## # Groups: p_overall [5]
## a p_overall p RR OR
## <int> <fct> <dbl> <dbl> <dbl>
## 1 60 5% 0.05 1.5 1.53
## 2 120 10% 0.1 1.5 1.57
## 3 240 20% 0.2 1.5 1.66
## 4 360 30% 0.3 1.5 1.78
## 5 600 50% 0.5 1.5 2.25df %>%
filter(round(RR, digits = 1) == 2) %>%
group_by(p_overall) %>%
filter(abs(RR-2) == min(abs(RR-2)))## # A tibble: 5 × 5
## # Groups: p_overall [5]
## a p_overall p RR OR
## <int> <fct> <dbl> <dbl> <dbl>
## 1 67 5% 0.05 2.03 2.10
## 2 133 10% 0.1 1.99 2.14
## 3 267 20% 0.2 2.01 2.37
## 4 400 30% 0.3 2 2.67
## 5 667 50% 0.5 2.00 4.01further learning
- Schmidt, C. O., & Kohlmann, T. (2008). When to use the odds ratio or the relative risk?. International journal of public health, 53(3), 165.
僕が今回描いたグラフがそのまま載っています。ちゃんと勉強したい人はおすすめ。 - Fuyama, K., Hagiwara, Y. & Matsuyama, Y. A simulation study of regression approaches for estimating risk ratios in the presence of multiple confounders. Emerg Themes Epidemiol 18, 18 (2021).
学部同期の論文 (ほんとすげえ) 。勉強したあとに読むと、非常に面白かったです。
最後まで読んでくださった方、本当におつかれさまでした。